Optimal packing

“How many candies are in the jar?” The typical quiz question sounds simple enough, but the underlying mathematics is surprisingly difficult. In fact, how to optimally pack objects of a certain shape in a given space is a longstanding mathematical problem. Even for something as seemingly simple as stacking spheres, the proof of the optimal arrangement took almost 400 years, from Johannes Kepler’s first idea in 1611 to a first mathematical proof announced by Thomas Hales in 1998. When one is not considering simple objects like spheres but more complex shapes, or even collections of objects of various sizes, the packing question gets even more difficult.

When “optimal” changes

Biophysicist Nico Schramma from the UvA Institute of Physics, together with Mazi Jalaal (also IoP) and Eric Weeks of Emory University, have been exploring a still more intricate packing challenge – but one that plants solve every day. The packing involved is that of chloroplasts, the tiny green organelles that capture sunlight for photosynthesis. Inside the cells of the water plant Elodea densa, disk-shaped chloroplasts must pack tightly to absorb as much light as possible. At the same time, they need enough freedom to shift around when light levels are too high, to prevent damage.

To investigate how these disk-like objects pack themselves optimally into the rectangular, brick-shaped spaces provided by the cells, the team combined computer simulations and theoretical computations. They discovered that only certain rectangular shapes allow chloroplasts to achieve both goals – efficient light capture at high chloroplast density, and enough space at the sides to harbour all chloroplasts during strong light avoidance. If the cell is flat and square-shaped, the chloroplasts fit well near the light-transmitting side, but not so well near the sides. If on the other hand the cell is too elongated, the opposite occurs. A cell geometry that optimizes both opposing targets must be at a sweet spot somewhere in between.

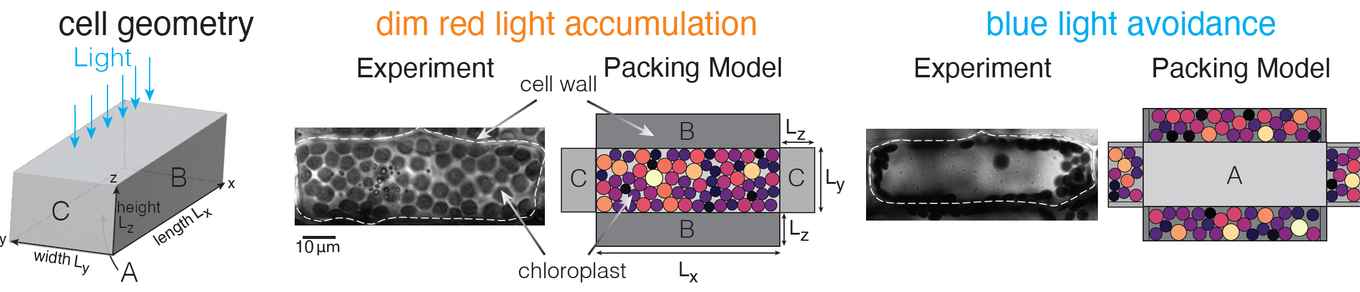
Nature’s solution

Strikingly, the natural geometry of Elodea cells matches the predicted optimal shapes very well. As for the number of chloroplasts within such a shape: the researchers found that they are not packed to the absolute maximum density but instead leave just enough room for slow rearrangements, resulting in a behaviour that can be compared to that of molecules in glasses.

Together, the clever choices of shape and density – evolution’s elegant solution to an intricate mathematical question – enable the Elodea densa cells to adapt between light-harvesting and light-avoidant states in an optimal manner. Future research will explore whether similar principles apply to other plants and their strategies for adapting to changing light.

Publication

Optimal disk packing of chloroplasts in plant cells, Nico Schramma, Eric Weeks and Maziyar Jalaal. Proc. Natl. Acad. Sci. U.S.A. (2025) 122 (43) e2511696122