Physicists rapport new breakthrough in field of topological matter
13 November 2020

In physics and mathematics, topology is the study of shapes and forms at large. Topology does not worry about fine details, but asks what can be learned about a system from its most global properties. For example, in topology, a donut and a wedding ring are essentially the same: both are solid shapes with a single hole. A pretzel, though, with two or three holes, would be considered a topologically different shape.
Bulk and boundary
Topology holds the promise of revolutionizing technologies in many fields, from quantum electronics to acoustics, and mechanics. Topology also plays a role in many materials. A fundamental property of topological matter is the so-called bulk-boundary correspondence: a simple topological quantity observed in the material’s interior can predict the emergence of waves localised at the material’s edges.
A well-known law of physics states that energy is conserved: it can be transformed from one form into another (by rolling a ball down a hill for example, changing gravitational energy into energy of motion) but it does not get lost or just appear from nowhere. However, this law only holds true in idealized systems that are perfectly isolated from their surroundings. In real life physical systems, energy does get lost, for example simply because it leaves (dissipates from) the system. Conversely, in materials science one now constructs ‘active materials’, which actually gain energy from their surroundings.
Recently, there has been an explosion of activity with the aim of generalizing the concept of topology to such more real-life systems where energy can be lost or injected. However, despite intense efforts, any behavior of topological edge waves in systems that do not conserve energy had not been observed experimentally. In a new paper that appeared in the journal Proceedings of the National Academy of Sciences this week, a team of physicists from the University of Amsterdam has now achieved two breakthroughs in this vibrant field.
From theory to material
First of all, the team discovered a novel form of bulk-boundary correspondence: a new relation between the interior of a material and what happens on its edge, particularly valid for these energy non-conserving systems. It was shown that a certain change in the topology inside the material, leads to a change of the locations of the wave-like effects on the edges.
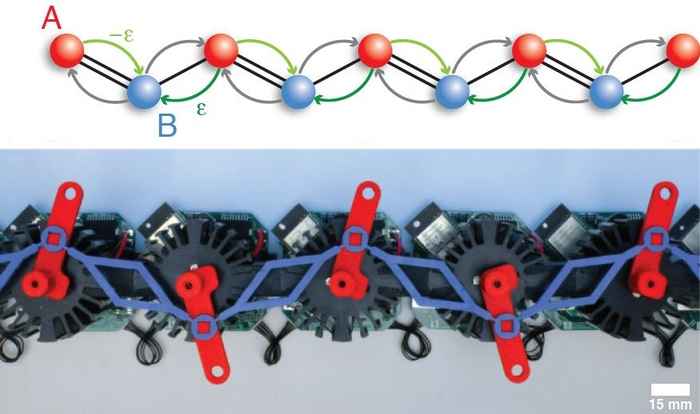
Secondly, the team made this theoretical finding very concrete by constructing, out of cog wheels, rods, levers and tiny robots, a specific metamaterial with the theoretically predicted property. In fact, the most favorable media to see the effect of topology on wave propagation are such metamaterials, which are composite systems artificially made as arrangements of identical units. The figure above shows an example, which is one-dimensional: every component only ‘talks’ to its left and right neighbours.
In idealized scenarios, each identical unit in such a metamaterial talks to its neighbours in a symmetric way, resulting in the conservation of energy. However, in the material constructed by the researchers, the units talk to their left and right neighbours in a different way. This makes the system gain or lose energy from or to the environment. The physicists now managed to show that even in this case, one can let waves travel through the system and topology then explains how these waves in the interior affect waves on the boundary. In particular, the topology of the setup determines on which side of the material these edge waves occur.
The work can have significant impact on many branches of physics, ranging from quantum mechanics for systems that are not in equilibrium to the construction of new and interesting metamaterials for situations where it is useful to engineer wave properties by steering waves on demand. Potential applications are in sensing or energy harvesting, or for example in creating new materials that very effectively damp or mitigate shocks and vibrations.
Reference
Observation of non-Hermitian topology and its bulk–edge correspondence in an active mechanical metamaterial, Ananya Ghatak, Martin Brandenbourger, Jasper van Wezel, and Corentin Coulais. Proceedings of the National Academy of Sciences, Nov 2020, 202010580.